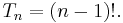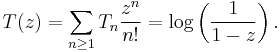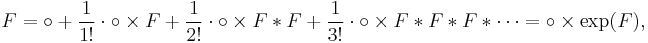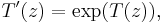Recursive tree

In graph theory, a discipline within mathematics, a recursive tree (i.e., unordered tree) is a non-planar labeled rooted tree. A size-n recursive tree is labeled by distinct integers 1, 2, ..., n, where the labels are strictly increasing starting at the root labeled 1. Recursive trees are non-planar, which means that the children of a particular node are not ordered. E.g. the following two size-three recursive trees are the same.

       1          1   
      / \   =    / \           
     /   \      /   \
    2     3    3     2

Recursive trees also appear in the literature under the name Increasing Cayley trees.

Contents

Properties

The number of size-n recursive trees is given by

T_n= (n-1)!. \,

Hence the exponential generating function T(z) of the sequence Tn is given by

T(z)= \sum_{n\ge 1} T_n \frac{z^n}{n!}=\log\left(\frac{1}{1-z}\right).

Combinatorically a recursive tree can be interpreted as a root followed by an unordered sequence of recursive trees. Let F denote the family of recursive trees.

F= \circ %2B \frac{1}{1!}\cdot \circ \times F %2B \frac{1}{2!}\cdot \circ \times F* F %2B \frac{1}{3!}\cdot \circ \times F* F* F * \cdots = \circ\times\exp(F),

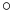where \circ denotes the node labeled by 1, × the Cartesian product and * the partition product for labeled objects.

By translation of the formal description one obtains the differential equation for T(z)

T'(z)= \exp(T(z)),

with T(0) = 0.

Bijections

There are bijective correspondences between recursive trees of size n and permutations of size n − 1.

Applications

Recursive trees can be generated using a simple stochastic process. Such random recursive trees are used as simple models for epidemics.

References